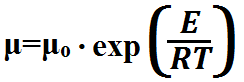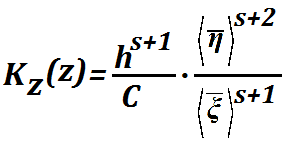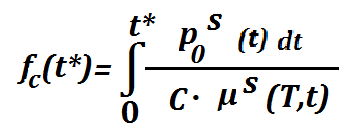Перколяционная модель консолидации слоев армированных термопластов

Введение. Высокопрочные изделия из армированных термопластов получают путем пултрузии, намотки, укладки, прессования. Прочность связи слоев, лент или стренг в этих процессах обеспечивается за счет их сплавления (консолидации). Для оптимизации условий формообразования изделий необходима модель, адекватно описывающая зависимость прочности связи слоев, лент или стренг от параметров процесса, поэтому исследованию механизма и режимов консолидации в последние годы уделяется большое внимание.

Согласно теории аутогезии ^[1] связь слоев термопластичного полимера обеспечивается за счет взаимной диффузии молекул при температурах, превышающих температуру плавления. Для взаимной диффузии молекул необходим близкий контакт слоев, который достигается в результате вязкого течения ^[2]. Указанные обстоятельства послужили основой для разработки двух моделей, наиболее распространенных в теории консолидации – диффузионной и деформационной. В данной работе излагается новый подход, основанный на предположении о том, что степень аутогезионной связи слоев армированных термопластов определяется глубиной затекания (перколяции) частиц полимера из одного слоя в другой.

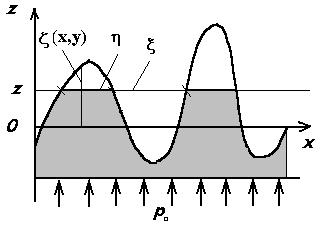
Модель. Пусть плоские в среднем (по крайней мере на участках, соизмеримых с размерами участков контакта) поверхности слоев имеют неровности, описываемые статически однородным нормальным случайным полем ζ(x, y) (рис.1). Начало отсчета по координате z совмещено со средней линией профиля, т. е. <ζ(x, y)> = 0. Здесь и далее <…> – оператор математического ожидания.

 Связь параметров распределения относительной ширины впадин и выступов, в частности, их средних значений  и как функции z (см. рис.1) с функцией распределения случайного поля ζ(x, y) известна из литературы ^[3]: = F(u);  = Q(u). Здесь F(u) – функция нормированного распределения величины ζ(x, y); Q(u) = 1 – F(u); u – относительная координата z: z = hu; (h – характерный размер, например высота неровностей).

Под действием давления p_o происходит затекание расплава полимера во впадины контактирующего с ним слоя. Предположим, что течение полимерного расплава подчиняется степенному закону τ=μ·ýⁿ, где τ – касательные напряжения; ý – скорость сдвига; μ – коэффициент консистенции; n – параметр среды. Примем зависимость коэффициента консистенции μ от термодинамической температуры Т в форме закона Аррениуса:

 где μ_o –константа; E – энергия активации вязкого течения; R – универсальная газовая постоянная.

Средняя скорость dz/dt проникновения полимера связана с градиентом давления уравнением перколяции (см., например, ^[4]):

 где P(z) – относительная площадь сечения впадин, которые заполняются полимером; K_z(z) – коэффициент проницаемости слоя в направлении z; p(z) – среднее давление на участках, заполняемых полимером; μ, – параметры закона течения полимерного расплава (s = 1/n).

В соответствии с капиллярной теорией затекания нелинейно-вязкой жидкости в пористый слой коэффициент проницаемости выражается через относительные размеры выступов и впадин соотношением:

 где h – высота неровностей; C – константа Козени; ,  – относительные размеры впадин и выступов как параметры распределения случайного поля ζ(x, y).

Величины P(z) и p(z) также зависят от параметров распределения размеров выступов и впадин, связанных в свою очередь с законом распределения случайного поля ζ(x, y), а именно: P(z)=; p(z)=p₀;

Относительная глубина затекания расплава u характеризует степень консолидации. При нормальном распределении случайного поля неровностей ζ(x, y) наибольшая относительная глубина впадин может быть принята равной 3. Долю от этой величины обозначим  степень консолидации c.

Подставим в уравнение (1) коэффициент проницаемости согласно формуле (2) и запишем величины, входящие в это уравнение, как функции z. Затем, разделяя переменные, проинтегрируем полученное уравнение. В результате получим следующее соотношение между степенью консолидации с*, температурой Т, приложенным давлением p_o и продолжительностью его действия t*:

  С другой стороны,           

            

при этом f_c(t*) = f(c*).

Выражение (3) связывает степень консолидации c*  со всеми основными параметрами процесса – давлением, температурой (через показатели вязкости расплава) и временем. Учитывается и изменение данных параметров в процессе консолидации. Для определения режимов, обеспечивающих достижение заданной степени консолидации c*, необходимо вычислить значение функции f(c*) по формуле (4), а затем, используя  уравнение (3), определить оптимальные параметры процесса.

Экспериментальная проверка

Адекватность модели проверяли, измеряя прочность  связи сплавленных между собой однонаправленно армированных лент. Ленты шириной 10±2 мм получали в результате пултрузионной пропитки стеклоровинга РБТ 13-2400 (30 % мас.) расплавами термопластичных полимеров – полиамида-6 (ПА-6) вторичного, полипропилена (ПП) марки каплен и полиэтилена низкого давления (ПЭНД). Варьировали температуру, давление и продолжительность консолидации.

Параметры закона течения полимерных расплавов определяли по методу сжатия дисков между плоскопараллельными плитами ^[5].Значения параметров вязкого течения расплавов и параметров процесса сплавления лент приведены в таблице.

 

Таблица 1:Параметры закона течения матричных полимеров и диапазон режимов консолидации лент

Матричный полимер	μo, Па∙сn	n	E, кДж/моль	рo, кПа	Т, ˚С	t*, c
ПА-6	7,1∙10-5	0,56	75,4	53-278	230-300	5-25
ПЭНД	7,6∙10-2	0,56	37,8	53-278	150-200	5-20
ПП	0,45	0,56	40,0	23-390	160-240	5-20

 Прочность связи лент оценивали по среднему напряжению межслойного сдвига τ`, соответствующему разрушающему усилию. Степень консолидации c* сплавленных между собой лент определяли как отношение τ` к максимальному значению прочности τ^*, соответствующему максимально достижимой прочности связи, для которой c* = 1.

На рис.2 показаны экспериментальные и рассчитанные по формулам (3) и (4) значения степени консолидации и функции fc(t*)  для различных матричных полимеров. Среднее квадратическое отклонение экспериментальных значений степени консолидации от расчетных менее 7%. Установлено также, что степень консолидации практически линейно зависит от логарифма функции fc(t*), т.е. от значения интеграла в правой части уравнения (3), содержащего все основные параметры процесса консолидации. Коэффициент корреляции между этими величинами равен 0,85, что свидетельствует о достаточно тесной статистической связи.

---

 

Выводы:

Предложена перколяционная модель консолидации слоев армированных термопластов. Результаты эксперимента подтверждают ее адекватность.

Модель может быть использована для определения оптимальных условий консолидации слоев, лент и стренг при изготовлении изделий путем пултрузии, намотки и укладки роликом.

---

 

 

 

Список литературы: Воюцкий С. С. Аутогезия высокополимеров. М., 1960. Lee W.T, Springer G.S.// J. of Composite Materials. 1978. Vol. 21. P. 1017-1055. Хусу А. П., Виттенберг Ю. Р., Пальмов В. А. Шероховатость поверхностей. Теоретико-вероятностный подход. М., 1975. Ставров В.П., Кременевская Е.И., Ставров В.В., Ткачев В.М. // Механика композитных материалов. 1997. № 4. С. 554-563. Ставров В.П., Дорожко А.В., Зуев А.П. и др. // Материалы, технологии, инструменты. 1998. № 3. С. 92-97.
Автор: О.И. Карпович, кандидат технических наук, доцент
Источник: УДК 678.073:678.027.9